KNN and K-means clustering

Gerko Vink

Erik-Jan van Kesteren

Methodology & Statistics @ Utrecht University

December 9, 2022

Packages and functions that we use

library(dplyr)    # Data manipulation
library(magrittr) # Pipes
library(ggplot2)  # Plotting suite
library(MASS)     # Dataset
library(class)    # K-nearest Neighbour
library(mvtnorm)  # Multivariate Normal tools


Custom theme for plots

helpIAmColourblind <- scale_color_manual(values = c("orange", 
                                                    "blue", 
                                                    "dark green"))

Supervised learning

We want to find the predictive function:

\[Y = f(X) + \epsilon \]

That minimizes \(\epsilon\) with respect to our goal.

  • Function \(f\) is an unknown, but fixed function of \(X = X1, \dots, Xp\)
  • \(p\) is the number of predictors
  • \(Y\) is the quantitative response
  • \(\epsilon \sim N(0, \sigma_\epsilon^2)\) is a random error term
  • \(\epsilon\) does not depend on \(X\)

Our aim is to find the \(f(X)\) that best represent the systematic information that \(X\) yields about \(Y\).

Supervised learning

With supervised learning every observation on our predictor

\[x_i, i=1, \dots, n\]

has a corresponding outcome measurement

\[y_i\] such that

\[\hat{y_i}=f({\bf x_i})\quad \text{and} \quad y_i = f({\bf x_i})+\epsilon_i.\]

Examples:

  • linear regression
  • logistic regression
  • k-nearest neighbours

Unsupervised learning

With unsupervised learning we have a vector of measurement \(\bf x_i\) for every unit \(i=1, \dots, n\), but we miss the associated response \(y_i\).

  1. There is no outcome to predict

    • Hence you cannot fit e.g. a linear regression model

  2. There is no outcome to verify the model

    • We lack the truth to supervise our analysis

What can we do?

Find patterns in \(\bf x_1, \dots, x_n\)

We can use this model to e.g. find out if some cases are more similar than other cases or which variables explain most of the variation

Examples:

  • Principal Components Analysis
  • k-means clustering

K-means and K-nearest neighbours

Two nonparametric algorithms

K-nearest neighbours (KNN)

  • supervised learning
  • prediction
  • classification

K-means clustering (kmeans)

  • unsupervised learning
  • dimension reduction / pattern recognition
  • clustering

Example dataset

Let’s create some data from a multivariate normal distribution

We start with fixing the random seed

set.seed(123)

and specifying the variance covariance matrix:

sigma <- matrix(c(1, .5, .5, 1), 2, 2)
rownames(sigma) <- colnames(sigma) <- c("x1", "x2")

Data relations

sigma
    x1  x2
x1 1.0 0.5
x2 0.5 1.0

Because the variances are 1, the resulting data will have a correlation of \[\rho = \frac{\text{cov}(y, x)}{\sigma_y\sigma_x} = \frac{.5}{1\times1} = .5.\]

Let’s draw the data

sim.data <- mvtnorm::rmvnorm(n     = 100, 
                             mean  = c(5, 5), 
                             sigma = sigma)
colnames(sim.data) <- c("x1", "x2")

Plot the data

sim.data %>% 
  as_tibble %>%
  ggplot(aes(x1, x2)) +
  geom_point()

Now add some clustering

sim.data <- 
  sim.data %>%
  as_tibble %>%
  mutate(class = sample(c("A", "B", "C"), size = 100, replace = TRUE))

We have added a new column that randomly assigns rows to level A, B or C

sim.data %>% head
# A tibble: 6 × 3
     x1    x2 class
  <dbl> <dbl> <chr>
1  4.40  4.63 C    
2  6.52  5.47 C    
3  5.57  6.69 C    
4  5.12  3.90 A    
5  4.22  4.39 A    
6  6.28  5.66 C

Plot the data again

sim.data %>%
  ggplot(aes(x1, x2,  colour = class)) +
  geom_point() + 
  helpIAmColourblind

Adjust the clusters to make them distinct

sim.data <- 
  sim.data %>%
  mutate(x2 = case_when(class == "A" ~ x2 + 1.5,
                        class == "B" ~ x2 - 1.5,
                        class == "C" ~ x2 + 1.5),
         x1 = case_when(class == "A" ~ x1 - 1.5,
                        class == "B" ~ x1 - 0,
                        class == "C" ~ x1 + 1.5))

The result: supervised

sim.data %>%
  ggplot(aes(x1, x2,  colour = class)) +
  geom_point() + 
  helpIAmColourblind

The result: unsupervised

sim.data %>%
  ggplot(aes(x1, x2)) +
  geom_point() + 
  helpIAmColourblind

K-Nearest Neighbors

How does it work?

  1. For every test observation \(x_0\) the \(K\) points that are close to \(x_0\) are identified.

  2. These closest points form set \(\mathcal{N}_0\).

  3. We estimate the probability for \(x_0\) being part of class \(j\) as the fraction of points in \(\mathcal{N}_0\) for whom the response equals \(j\): \[P(Y = j | X = x_0) = \frac{1}{K}\sum_{i\in\mathcal{N}_0}I(y_i=j)\]

  4. The observation \(x_0\) is classified to the class with the largest probability

In short

An observation gets that class assigned to which most of its \(K\) neighbours belong

Why KNN?

Because \(X\) is assigned to the class to which most of the observations belong it is

  • non-parametric

    • no assumptions about the distributions, or the shape of the decision boundary

  • expected to be far better than logistic regression when decision boundaries are non-linear

However, we do not get parameters as with LDA and regression.

  • We thus cannot determine the relative importance of predictors
  • The “model” == the existing observations: instance-based learning

Fitting a K-NN model

First we need to determine a training set

set.seed(123)
sim.data <-
  sim.data %>% 
  mutate(set = sample(c("Train", "Test"), size = 100, 
                      prob = c(.25, .75), replace = TRUE))
sim.data
# A tibble: 100 × 4
      x1    x2 class set  
   <dbl> <dbl> <chr> <chr>
 1  5.90  6.13 C     Test 
 2  8.02  6.97 C     Train
 3  7.07  8.19 C     Test 
 4  3.62  5.40 A     Train
 5  2.72  5.89 A     Train
 6  7.78  7.16 C     Test 
 7  5.42  3.71 B     Test 
 8  6.43  8.08 C     Train
 9  4.97  1.73 B     Test 
10  4.06  6.22 A     Test 
# … with 90 more rows

Fitting a K-NN model

Then we split the data into a training (build the model) and a test (verify the model) set

train.data <- subset(sim.data, set == "Train", select = c(x1, x2))
test.data <-  subset(sim.data, set == "Test",  select = c(x1, x2))
obs.class <-  subset(sim.data, set == "Train", select = class)

Now we can fit the K-NN model

fit.knn <- knn(train = train.data,
               test  = test.data, 
               cl    = as.matrix(obs.class),
               k     = 3)
fit.knn
 [1] C C C B B A B B A A C C A A C A A C C C B C C B B A B B B B A B A B A C A C
[39] C B C C C A A C B C B A A B B C C A B B C C C B A B B C B A C A C B A
Levels: A B C

Predictions

class.test <- subset(sim.data, set == "Test", select = class) %>%
  as.matrix()
correct <- fit.knn == class.test
mean(correct)
[1] 0.9589041
table(fit.knn, class.test)
       class.test
fit.knn  A  B  C
      A 21  0  0
      B  0 24  1
      C  0  2 25

The (in)correct responses KNN = 3

cbind(test.data, correct) %>%
  ggplot(aes(x1, x2,  colour = correct)) +
  geom_point() +
  scale_colour_manual(values = c("red", "black"))

Fewer neighbours

fit.knn <- knn(train = train.data,
               test  = test.data, 
               cl    = as.matrix(obs.class),
               k     = 2)
correct <- fit.knn == class.test
mean(correct)
[1] 0.9452055
table(fit.knn, class.test)
       class.test
fit.knn  A  B  C
      A 21  1  1
      B  0 23  0
      C  0  2 25

More neighbours

fit.knn <- knn(train = train.data,
               test  = test.data, 
               cl    = as.matrix(obs.class),
               k     = 4)
correct <- fit.knn == class.test
mean(correct)
[1] 0.9452055
table(fit.knn, class.test)
       class.test
fit.knn  A  B  C
      A 21  0  1
      B  0 24  1
      C  0  2 24

Even more neighbours

fit.knn <- knn(train = train.data,
               test = test.data, 
               cl = as.matrix(obs.class),
               k = 10)
correct <- fit.knn == class.test
mean(correct)
[1] 0.890411
table(fit.knn, class.test)
       class.test
fit.knn  A  B  C
      A 21  1  5
      B  0 25  2
      C  0  0 19

The (in)correct responses KNN = 10

cbind(test.data, correct) %>%
  ggplot(aes(x1, x2,  colour = correct)) +
  geom_point() +
  scale_colour_manual(values = c("red", "black"))

Predicting a new observation

Let’s make a new observation:

newObs <- data.frame(x1 = 5.5, x2 = 4.5)

Predicting a new observation

Predicting a new observation

Now we predict the class of this new observation, using the entire data for training our model

knn(train = sim.data[, 1:2], cl = sim.data$class, k = 10, test = newObs)
[1] B
Levels: A B C

K-means clustering

Remember: unsupervised

sim.data %>%
  ggplot(aes(x1, x2)) +
  geom_point()

Goal: finding clusters in our data

K-means clustering partitions our dataset into \(K\) distinct, non-overlapping clusters or subgroups.

What is a cluster?

A set of relatively similar observations.

What is “relatively similar”?

This is up to the programmer/researcher to decide. For example, we can say the “within-class” variance is as small as possible and the between-class variance as large as possible.

Why perform clustering?

We expect clusters in our data, but weren’t able to measure them

  • potential new subtypes of cancer tissue

We want to summarise features into a categorical variable to use in further decisions/analysis

  • subgrouping people by their spending types

The k-means algorithm

  1. Randomly assign values to K classes
  2. Calculate the centroid (colMeans) for each class
  3. Assign each value to its closest centroid class
  4. If the assignments changed, go to step 2. else stop.

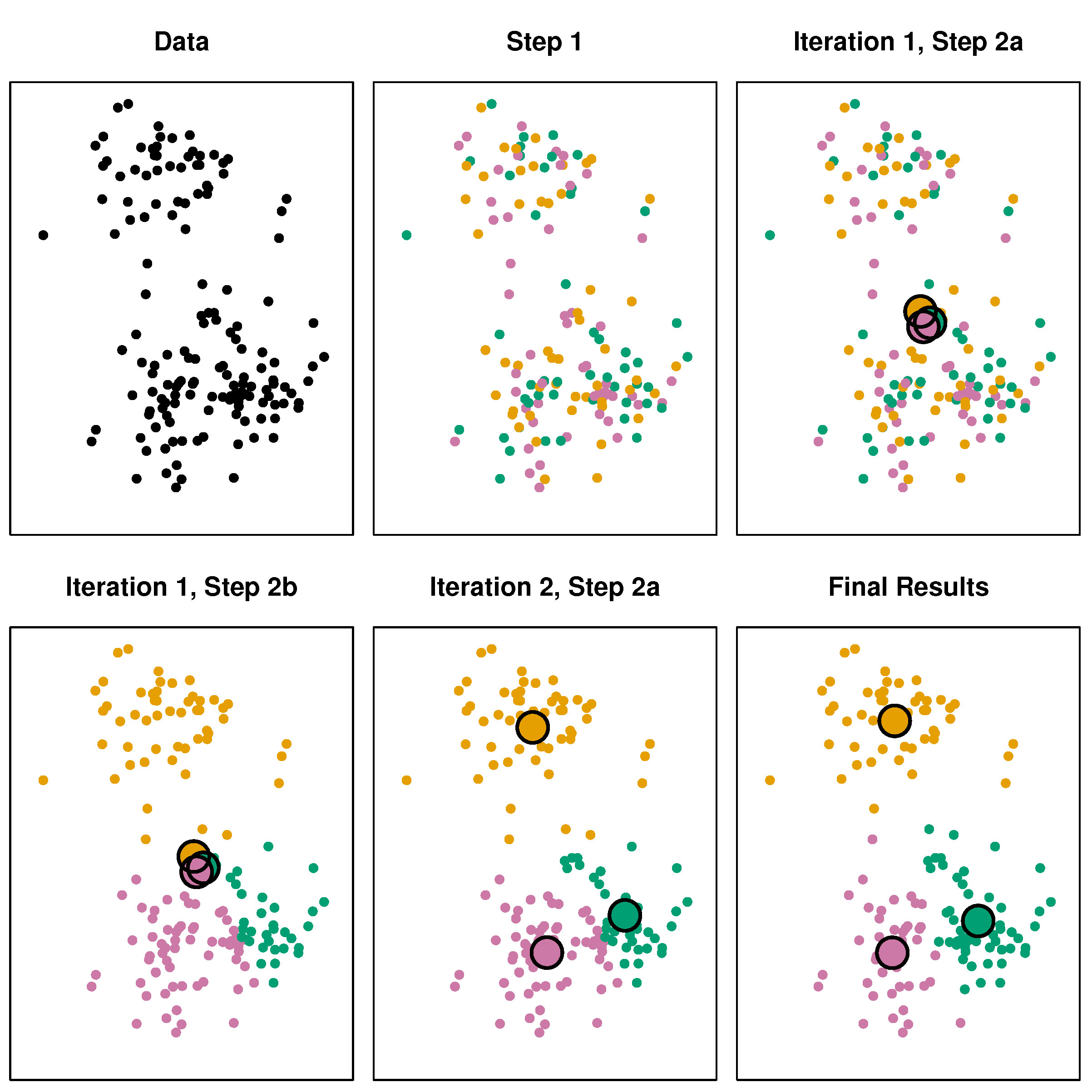
Source: James, G., Witten, D., Hastie, T., & Tibshirani, R. (2013). An introduction to statistical learning (Vol. 112). New York: Springer.

The k-means algorithm

K is a tuning parameter (centers)

(fitkm <- kmeans(sim.data[, 1:2], centers = 3))
K-means clustering with 3 clusters of sizes 39, 35, 26

Cluster means:
        x1       x2
1 4.994727 3.532014
2 3.591445 6.394369
3 6.845077 6.976240

Clustering vector:
  [1] 3 3 3 2 2 3 1 3 1 2 1 1 1 2 2 2 3 3 2 2 3 2 3 1 2 2 3 1 2 1 2 1 3 1 3 1 2
 [38] 1 2 1 1 1 1 2 1 2 1 2 3 1 2 3 1 1 1 3 2 2 1 1 2 2 3 1 3 1 1 1 2 1 2 2 2 1
 [75] 1 3 3 2 1 1 3 3 3 3 1 2 2 1 2 1 1 3 1 2 3 2 2 3 1 2

Within cluster sum of squares by cluster:
[1] 49.33578 46.51667 49.21032
 (between_SS / total_SS =  73.0 %)

Available components:

[1] "cluster"      "centers"      "totss"        "withinss"     "tot.withinss"
[6] "betweenss"    "size"         "iter"         "ifault"

The result:

sim.data$clust <- as.factor(fitkm$cluster)

sim.data %>% ggplot +
  geom_point(aes(x = x1, y = x2, colour = clust)) +
  helpIAmColourblind

Comparison

# this is the data-generating class

sim.data %>% ggplot +
  geom_point(aes(x = x1, y = x2, colour = class)) +
  helpIAmColourblind

Centroids

sim.data %>% ggplot +
  geom_point(aes(x = x1, y = x2, colour = clust)) +
  geom_point(aes(x = x1, y = x2), data = as.data.frame(fitkm$centers),
             size = 5, col = "red", alpha = 0.8) +
  helpIAmColourblind

K = 5

K = 2

Gerko Vink