How wrong may a useful model be?

Gerko Vink

Methodology & Statistics @ Utrecht University

December 9, 2022

We use the following packages

library(MASS)
library(dplyr)
library(magrittr)
library(ggplot2)
library(mice)
library(DAAG)
library(caret)

The linear model

Notation

The mathematical formulation of the relationship between variables can be written as

\[ \mbox{observed}=\mbox{predicted}+\mbox{error} \]

or (for the greek people) in notation as \[y=\mu+\varepsilon\]

where

\(\mu\) (mean) is the part of the outcome that is explained by model
\(\varepsilon\) (residual) is the part of outcome that is not explained by model

Univariate expectation

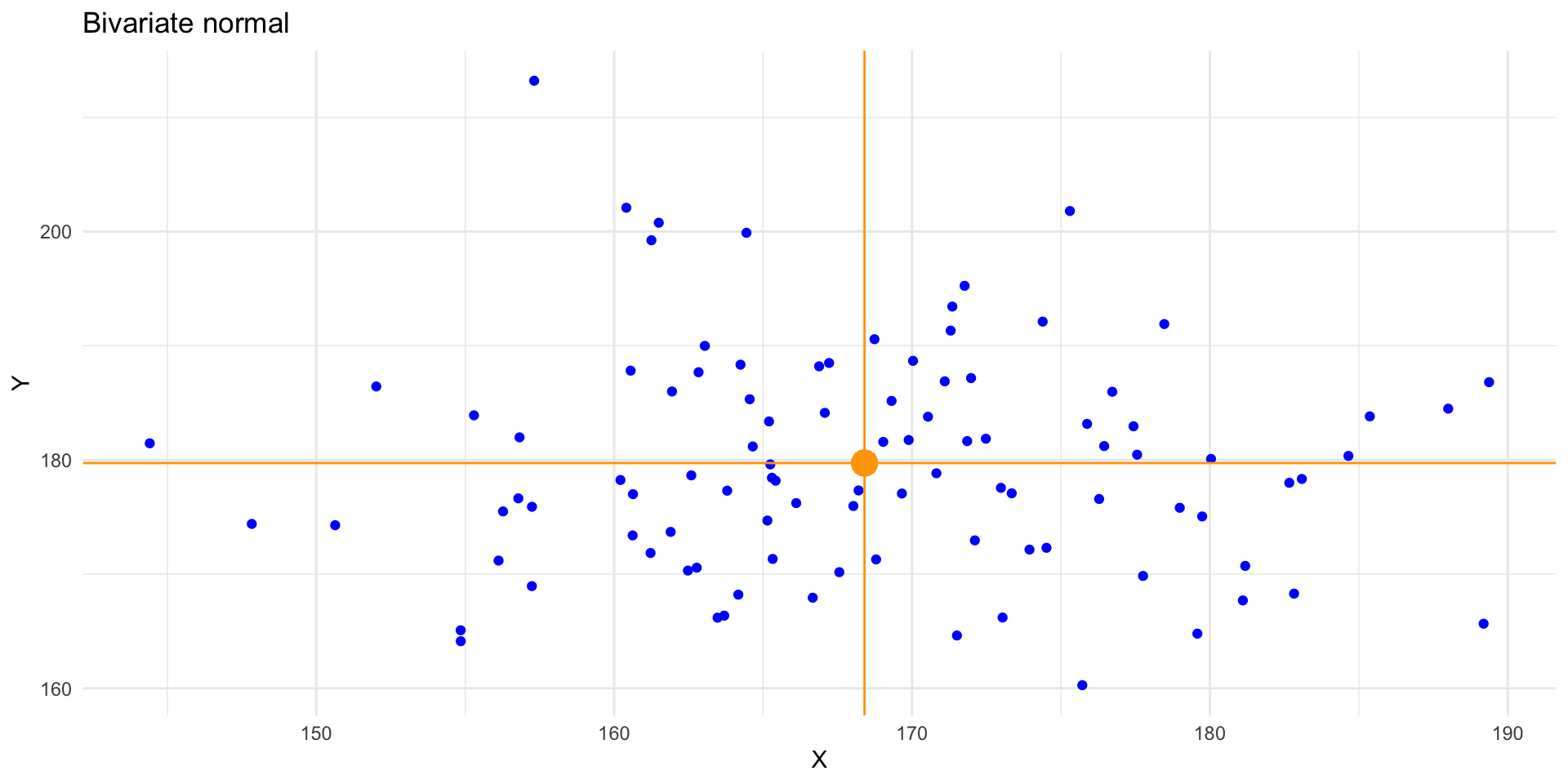
Conditional expectation

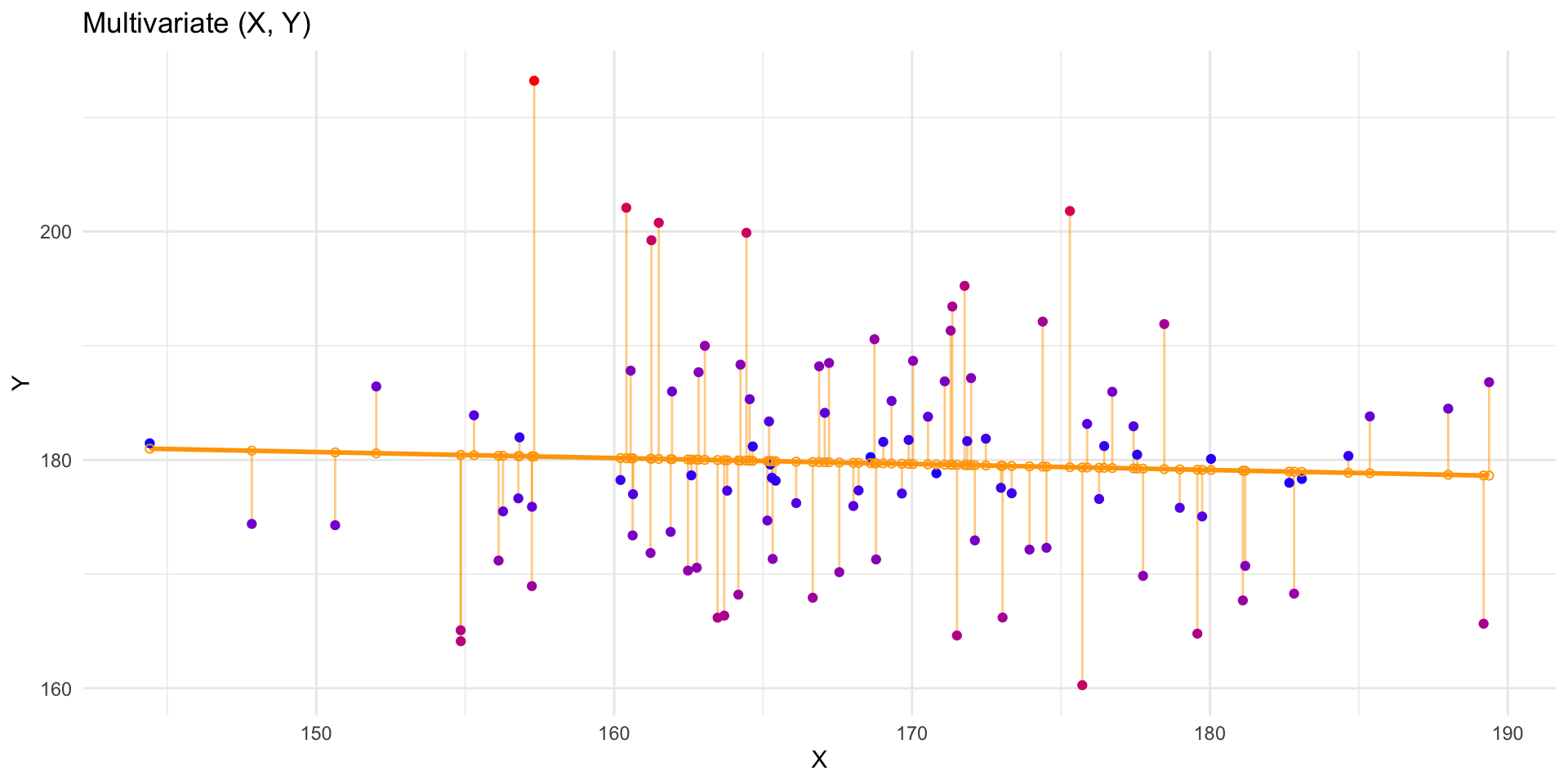
Assumptions

The key assumptions

There are four key assumptions about the use of linear regression models.

In short, we assume

The outcome to have a linear relation with the predictors and the predictor relations to be additive.
- the expected value for the outcome is a straight-line function of each predictor, given that the others are fixed.
- the slope of each line does not depend on the values of the other predictors
- the effects of the predictors on the expected value are additive
\[ y = \alpha + \beta_1X_1 + \beta_2X_2 + \beta_3X_3 + \epsilon\]
The residuals are statistically independent
The residual variance is constant
- accross the expected values
- across any of the predictors
The residuals are normally distributed with mean \(\mu_\epsilon = 0\)

A simple model

fit <- anscombe %$%
  lm(y1 ~ x1)
fit


Call:
lm(formula = y1 ~ x1)

Coefficients:
(Intercept)           x1  
     3.0001       0.5001

fit2 <- anscombe %$%
  lm(y2 ~ x2)

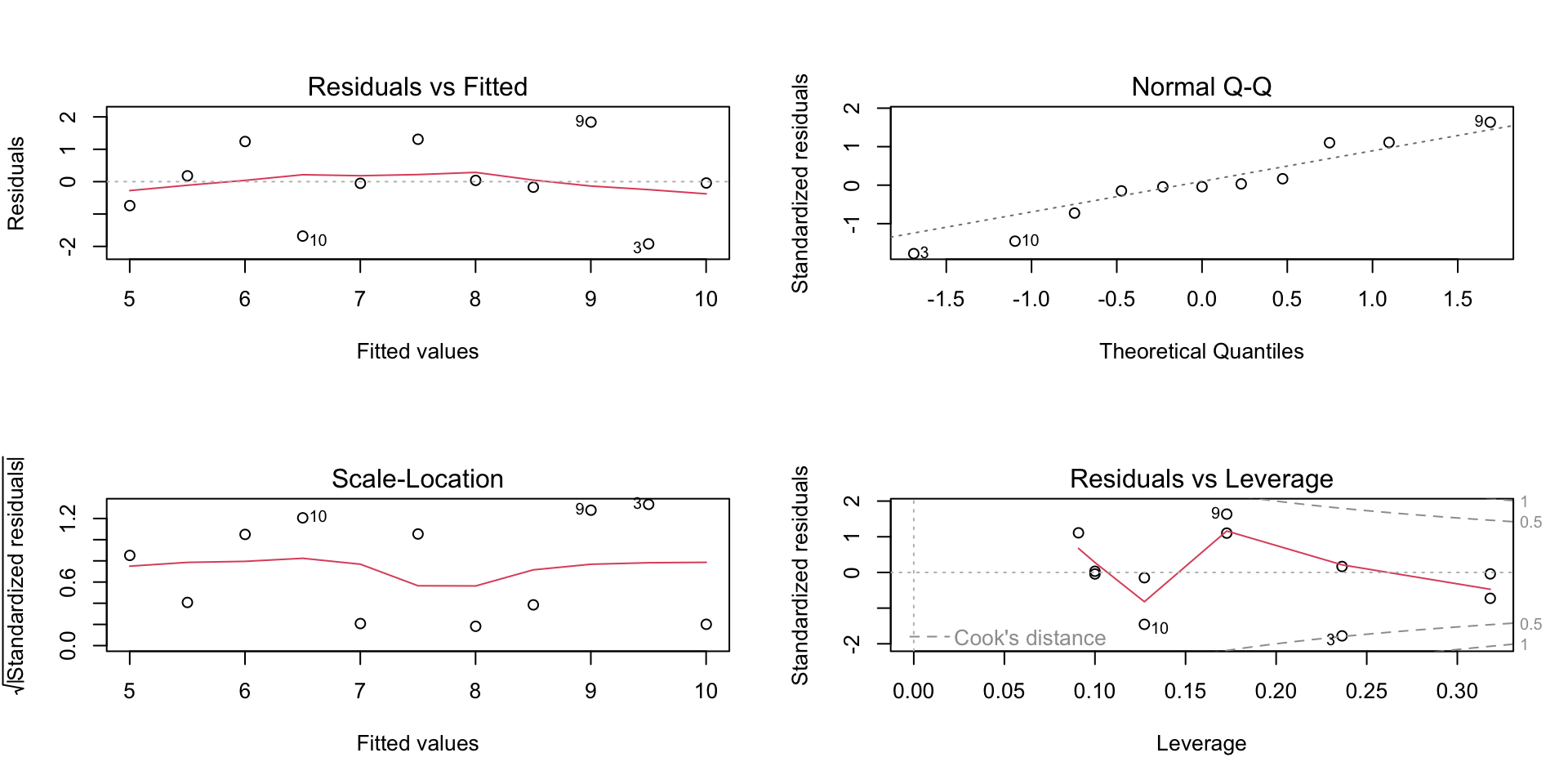
Visualizing the assumptions

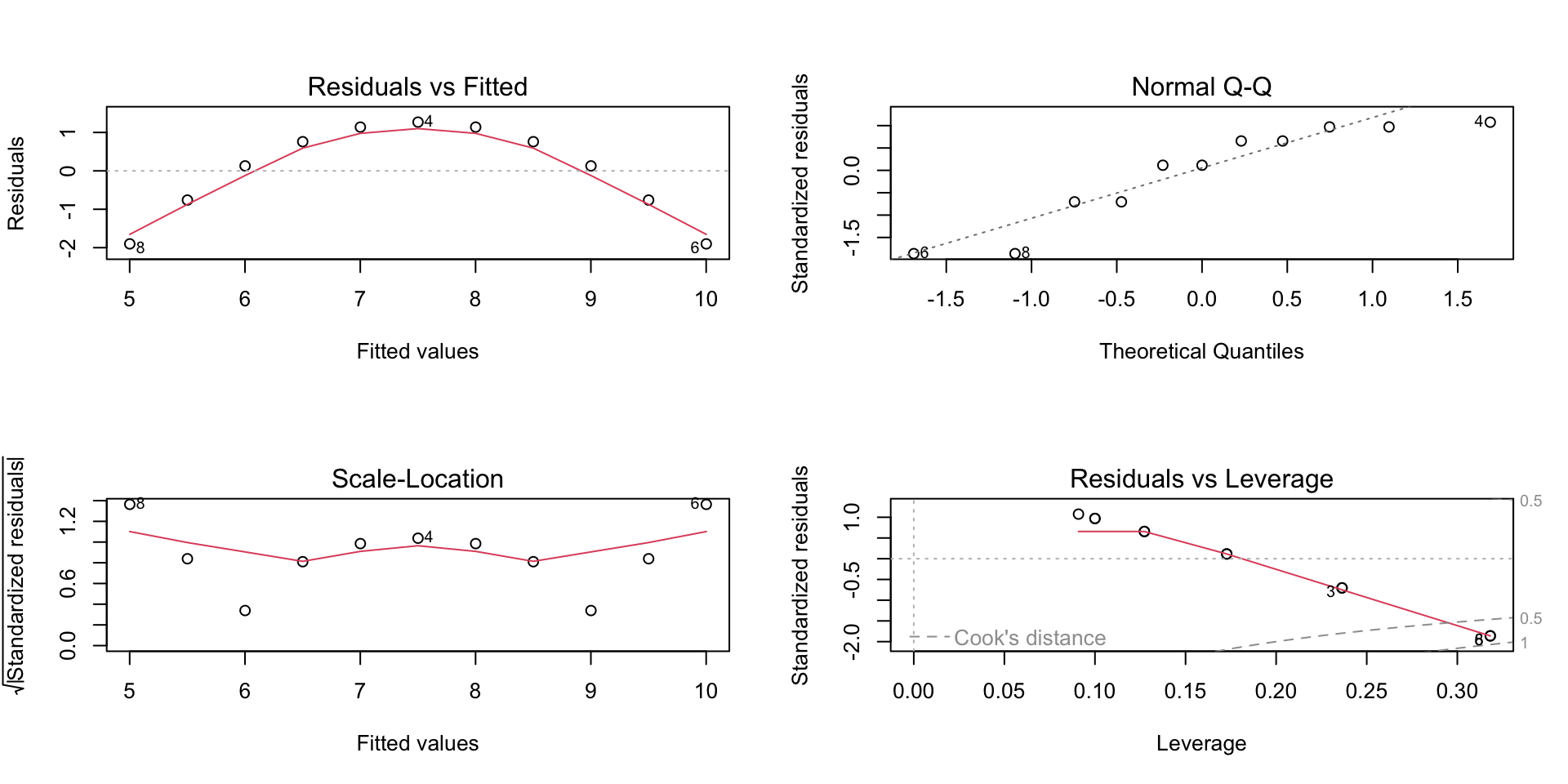
Model fit

A simple model

boys.fit <- 
  na.omit(boys) %$% # Extremely wasteful
  lm(age ~ reg)
boys.fit


Call:
lm(formula = age ~ reg)

Coefficients:
(Intercept)      regeast      regwest     regsouth      regcity  
    14.7109      -0.8168      -0.7044      -0.6913      -0.6663

boys %>% na.omit(boys) %$% aggregate(age, list(reg), mean)

  Group.1        x
1   north 14.71094
2    east 13.89410
3    west 14.00657
4   south 14.01965
5    city 14.04460

Plotting the model

means <- boys %>% na.omit(boys) %>% group_by(reg) %>% summarise(age = mean(age))
ggplot(na.omit(boys), aes(x = reg, y = age)) + 
  geom_point(color = "grey") + 
  geom_point(data = means, stat = "identity", size = 3)

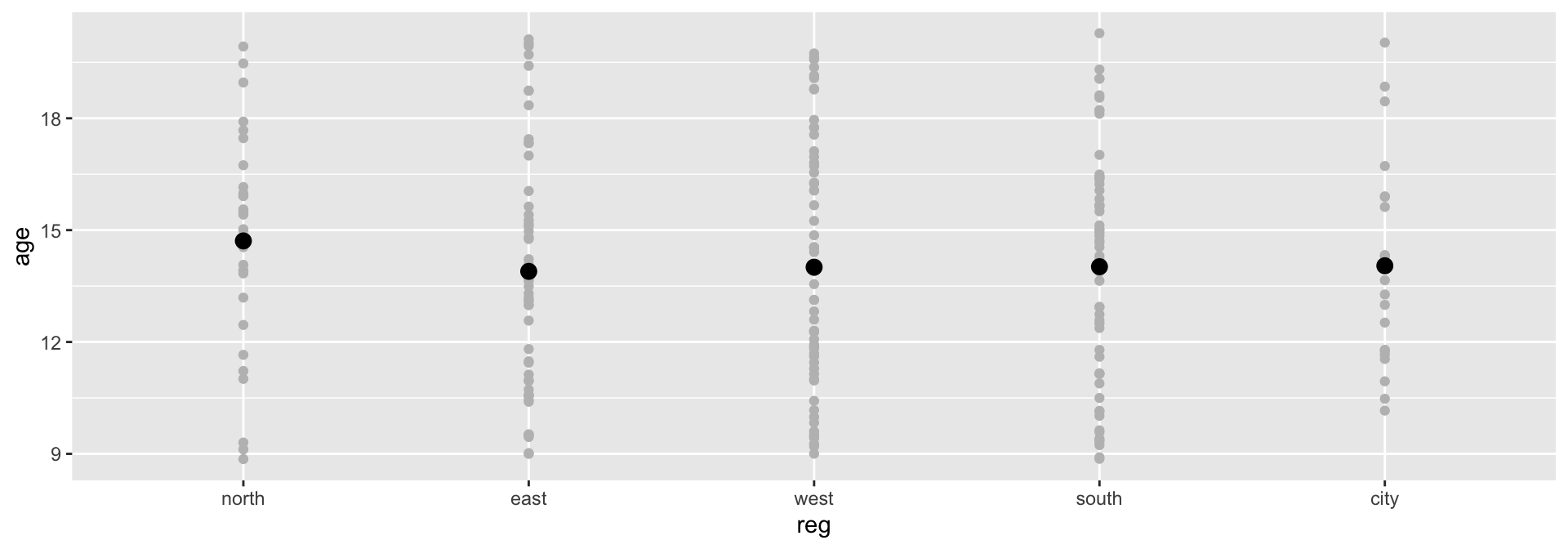
Model parameters

boys.fit %>%
  summary()


Call:
lm(formula = age ~ reg)

Residuals:
    Min      1Q  Median      3Q     Max 
-5.8519 -2.5301  0.0254  2.2274  6.2614 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  14.7109     0.5660  25.993   <2e-16 ***
regeast      -0.8168     0.7150  -1.142    0.255    
regwest      -0.7044     0.6970  -1.011    0.313    
regsouth     -0.6913     0.6970  -0.992    0.322    
regcity      -0.6663     0.9038  -0.737    0.462    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.151 on 218 degrees of freedom
Multiple R-squared:  0.006745,  Adjusted R-squared:  -0.01148 
F-statistic: 0.3701 on 4 and 218 DF,  p-value: 0.8298

Scientific notation

If you have trouble reading scientific notation, 2e-16 means the following

\[2\text{e-16} = 2 \times 10^{-16} = 2 \times (\frac{1}{10})^{-16}\]

This indicates that the comma should be moved 16 places to the left:

\[2\text{e-16} = 0.0000000000000002\]

Is it a good model?

boys.fit %>%
  anova()

Analysis of Variance Table

Response: age
           Df Sum Sq Mean Sq F value Pr(>F)
reg         4   14.7  3.6747  0.3701 0.8298
Residuals 218 2164.6  9.9293

It is not a very informative model. The anova is not significant, indicating that the contribution of the residuals is larger than the contribution of the model.

The outcome age does not change significantly when reg is varied.

AIC

Akaike’s An Information Criterion

boys.fit %>% 
  AIC()

[1] 1151.684

What is AIC

AIC comes from information theory and can be used for model selection. The AIC quantifies the information that is lost by the statistical model, through the assumption that the data come from the same model. In other words: AIC measures the fit of the model to the data.

The better the fit, the less the loss in information
AIC works on the log scale:
- \(\text{log}(0) = -\infty\), \(\text{log}(1) = 0\), etc.
the closer the AIC is to \(-\infty\), the better

Model comparison

A new model

Let’s add predictor hgt to the model:

boys.fit2 <- 
  na.omit(boys) %$%
  lm(age ~ reg + hgt)

boys.fit %>% AIC()

[1] 1151.684

boys.fit2 %>% AIC()

[1] 836.3545

Another model

Let’s add wgt to the model

boys.fit3 <- 
  na.omit(boys) %$%
  lm(age ~ reg + hgt + wgt)

And another model

Let’s add wgt and the interaction between wgt and hgt to the model

boys.fit4 <- 
  na.omit(boys) %$%
  lm(age ~ reg + hgt * wgt)

is equivalent to

boys.fit4 <- 
  na.omit(boys) %$%
  lm(age ~ reg + hgt + wgt + hgt:wgt)

Model comparison

AIC(boys.fit, boys.fit2, boys.fit3, boys.fit4)

          df       AIC
boys.fit   6 1151.6839
boys.fit2  7  836.3545
boys.fit3  8  822.4164
boys.fit4  9  823.0386

And with `anova()`

anova(boys.fit, boys.fit2, boys.fit3, boys.fit4)

Analysis of Variance Table

Model 1: age ~ reg
Model 2: age ~ reg + hgt
Model 3: age ~ reg + hgt + wgt
Model 4: age ~ reg + hgt * wgt
  Res.Df     RSS Df Sum of Sq        F    Pr(>F)    
1    218 2164.59                                    
2    217  521.64  1   1642.94 731.8311 < 2.2e-16 ***
3    216  485.66  1     35.98  16.0276 8.595e-05 ***
4    215  482.67  1      2.99   1.3324    0.2497    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Inspect `boys.fit3`

boys.fit3 %>% anova()

Analysis of Variance Table

Response: age
           Df  Sum Sq Mean Sq  F value    Pr(>F)    
reg         4   14.70    3.67   1.6343    0.1667    
hgt         1 1642.94 1642.94 730.7065 < 2.2e-16 ***
wgt         1   35.98   35.98  16.0029 8.688e-05 ***
Residuals 216  485.66    2.25                       
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Inspect `boys.fit4`

boys.fit4 %>% anova()

Analysis of Variance Table

Response: age
           Df  Sum Sq Mean Sq  F value    Pr(>F)    
reg         4   14.70    3.67   1.6368    0.1661    
hgt         1 1642.94 1642.94 731.8311 < 2.2e-16 ***
wgt         1   35.98   35.98  16.0276 8.595e-05 ***
hgt:wgt     1    2.99    2.99   1.3324    0.2497    
Residuals 215  482.67    2.24                       
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

It seems that reg and the interaction hgt:wgt are redundant

Remove `reg`

boys.fit5 <- 
  na.omit(boys) %$%
  lm(age ~ hgt + wgt)

Let’s revisit the comparison

anova(boys.fit, boys.fit2, boys.fit3, boys.fit5)

Analysis of Variance Table

Model 1: age ~ reg
Model 2: age ~ reg + hgt
Model 3: age ~ reg + hgt + wgt
Model 4: age ~ hgt + wgt
  Res.Df     RSS Df Sum of Sq        F    Pr(>F)    
1    218 2164.59                                    
2    217  521.64  1   1642.94 730.7065 < 2.2e-16 ***
3    216  485.66  1     35.98  16.0029 8.688e-05 ***
4    220  492.43 -4     -6.77   0.7529    0.5571    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

The boys.fit5 model is better than the previous model - it has fewer parameters

Influence of cases

DfBeta calculates the change in coefficients depicted as deviation in SE’s.

boys.fit5 %>%
  dfbeta() %>%
  head(n = 7)

  (Intercept)           hgt           wgt
1  0.08023815 -0.0006010829  3.886307e-04
2 -0.16849516  0.0011153227 -4.813872e-04
3 -0.08258333  0.0005122980 -1.222825e-04
4 -0.04399686  0.0002530928 -8.689133e-06
5 -0.28701562  0.0021630263 -1.581283e-03
6 -0.06116123  0.0002818449  1.652042e-04
7 -0.04791078  0.0002228673  1.274280e-04

Prediction

Fitted values

Let’s use the simpler anscombe data example

fit <- anscombe %$% lm(y1 ~ x1)

y_hat <- 
  fit %>%
  fitted.values()

The residual is then calculated as

y_hat - anscombe$y1

          1           2           3           4           5           6 
-0.03900000  0.05081818  1.92127273 -1.30909091  0.17109091  0.04136364 
          7           8           9          10          11 
-1.23936364  0.74045455 -1.83881818  1.68072727 -0.17945455

Predict new values

If we introduce new values for the predictor x1, we can generate predicted values from the model

new.x1 <- data.frame(x1 = 1:20)
fit %>% predict(newdata = new.x1)

        1         2         3         4         5         6         7         8 
 3.500182  4.000273  4.500364  5.000455  5.500545  6.000636  6.500727  7.000818 
        9        10        11        12        13        14        15        16 
 7.500909  8.001000  8.501091  9.001182  9.501273 10.001364 10.501455 11.001545 
       17        18        19        20 
11.501636 12.001727 12.501818 13.001909

Predictions are draws from the regression line

pred <- fit %>% predict(newdata = new.x1)
lm(pred ~ new.x1$x1)$coefficients

(Intercept)   new.x1$x1 
  3.0000909   0.5000909

fit$coefficients

(Intercept)          x1 
  3.0000909   0.5000909

Prediction intervals

fit %>% predict(interval = "prediction")

         fit      lwr       upr
1   8.001000 5.067072 10.934928
2   7.000818 4.066890  9.934747
3   9.501273 6.390801 12.611745
4   7.500909 4.579129 10.422689
5   8.501091 5.531014 11.471168
6  10.001364 6.789620 13.213107
7   6.000636 2.971271  9.030002
8   5.000455 1.788711  8.212198
9   9.001182 5.971816 12.030547
10  6.500727 3.530650  9.470804
11  5.500545 2.390073  8.611017

A prediction interval reflects the uncertainty around a single value. The confidence interval reflects the uncertainty around the mean prediction values.

Assessing predictive accuracy

Model performance

fit %>% 
  predict() %>% 
  caret::postResample(anscombe$y1)

     RMSE  Rsquared       MAE 
1.1185498 0.6665425 0.8374050

These performance measures only give us estimates about the training error.

Always use at least crossvalidation to evaluate predictive performance.

K-fold cross-validation

Divide sample in \(k\) mutually exclusive training sets
Do for all \(j\in\{1,\dots,k\}\) training sets
1. fit model to training set \(j\)
2. obtain predictions for test set \(j\) (remaining cases)
3. compute residual variance (MSE) for test set \(j\)
Compare MSE in cross-validation with MSE in sample
Small difference suggests good predictive accuracy

The original model

fit %>% summary()


Call:
lm(formula = y1 ~ x1)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.92127 -0.45577 -0.04136  0.70941  1.83882 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)   
(Intercept)   3.0001     1.1247   2.667  0.02573 * 
x1            0.5001     0.1179   4.241  0.00217 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.237 on 9 degrees of freedom
Multiple R-squared:  0.6665,    Adjusted R-squared:  0.6295 
F-statistic: 17.99 on 1 and 9 DF,  p-value: 0.00217

K-fold cross-validation `anscombe` data

DAAG::CVlm(anscombe, fit, plotit=F, printit=T)


fold 1 
Observations in test set: 3 
                     5        7        11
x1          11.0000000 6.000000 5.0000000
cvpred       8.4432584 5.585955 5.0144944
y1           8.3300000 7.240000 5.6800000
CV residual -0.1132584 1.654045 0.6655056

Sum of squares = 3.19    Mean square = 1.06    n = 3 

fold 2 
Observations in test set: 4 
                    2          6         8        10
x1           8.000000 14.0000000  4.000000  7.000000
cvpred       7.572234  9.6808511  6.166489  7.220798
y1           6.950000  9.9600000  4.260000  4.820000
CV residual -0.622234  0.2791489 -1.906489 -2.400798

Sum of squares = 9.86    Mean square = 2.47    n = 4 

fold 3 
Observations in test set: 4 
                     1         3        4         9
x1          10.0000000 13.000000 9.000000 12.000000
cvpred       7.8397519  9.367405 7.330534  8.858187
y1           8.0400000  7.580000 8.810000 10.840000
CV residual  0.2002481 -1.787405 1.479466  1.981813

Sum of squares = 9.35    Mean square = 2.34    n = 4 

Overall (Sum over all 4 folds) 
      ms 
2.036958

K-fold cross-validation `anscombe` data

residual variance sample is \(1.24^2 \approx 1.53\)
residual variance cross-validation is 2.04
regression lines in the 3 folds are similar

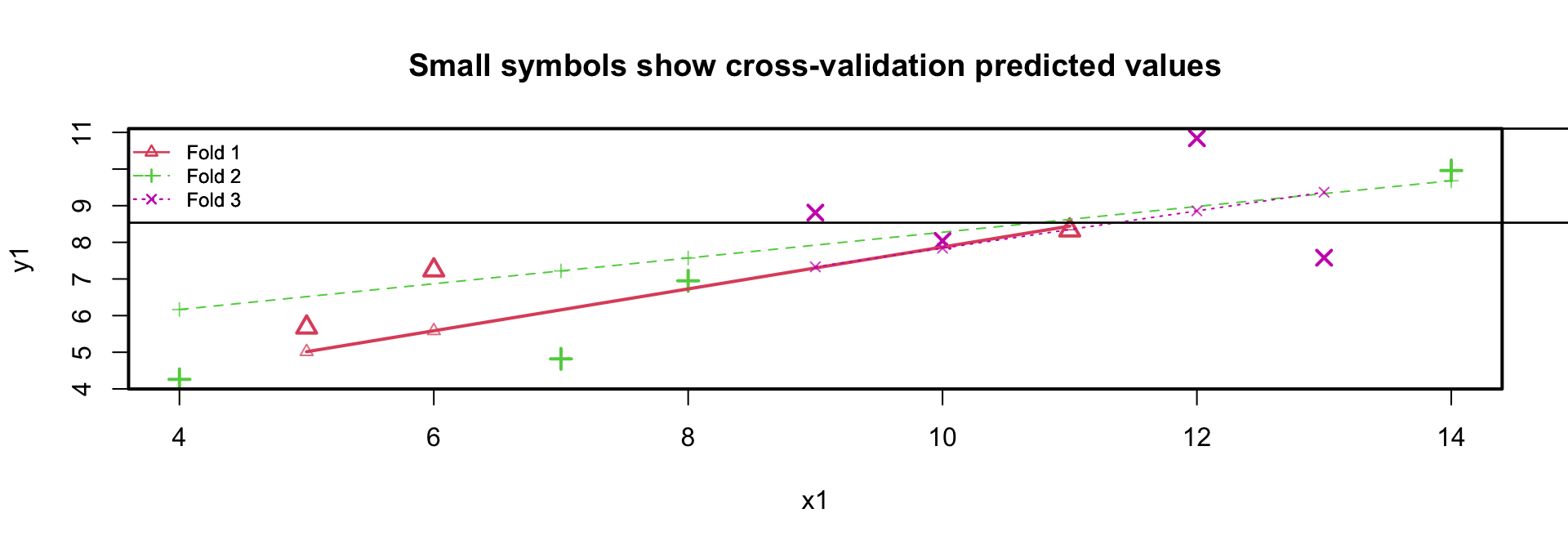
DAAG::CVlm(anscombe, fit, plotit="Observed", printit=F)

Plotting the residuals

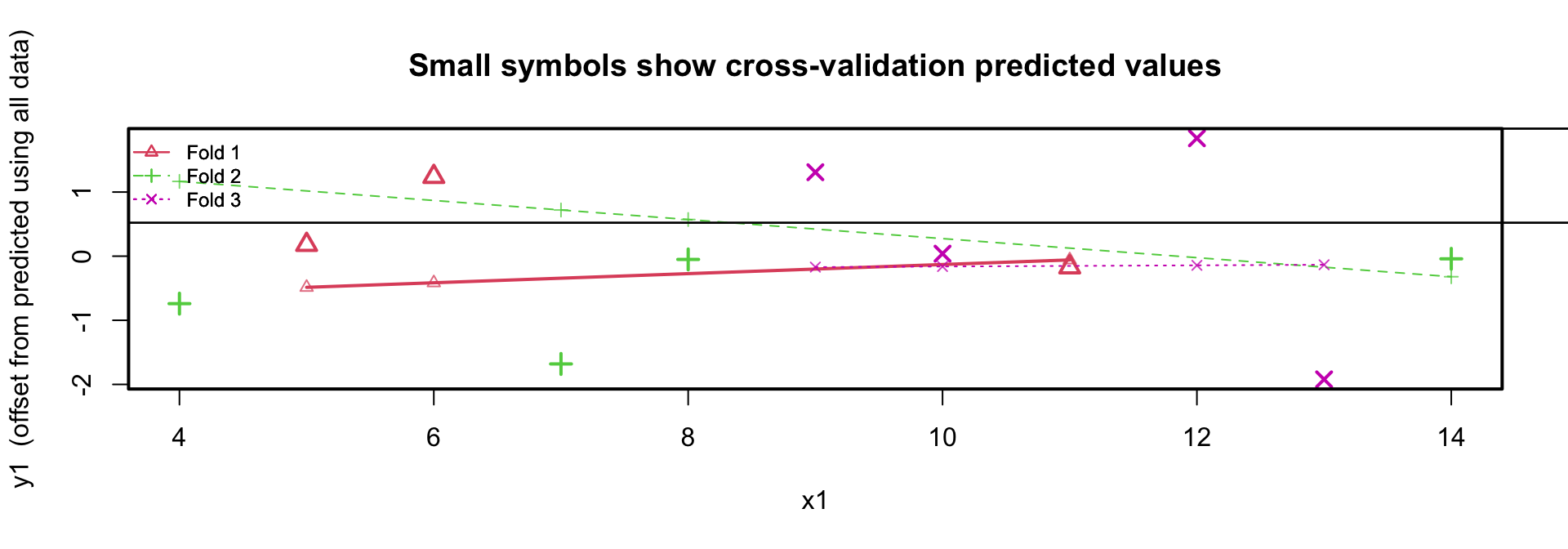
DAAG::CVlm(anscombe, fit, plotit="Residual", printit=F)

K-fold cross-validation `boys` data

residual variance sample is \(1.496^2 \approx 2.24\)
residual variance cross-validation is 2.28
regression lines in the 3 folds almost identical

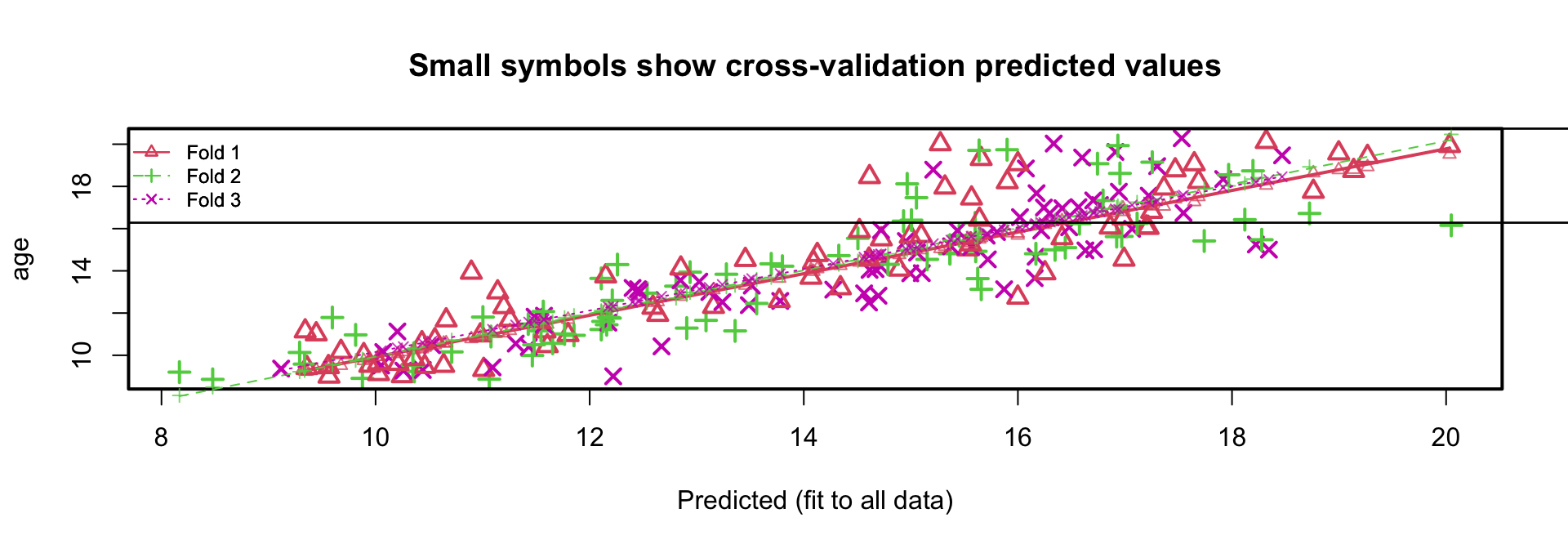
DAAG::CVlm(na.omit(boys), boys.fit5, plotit="Observed", printit=F)

K-fold cross-validation `boys` data

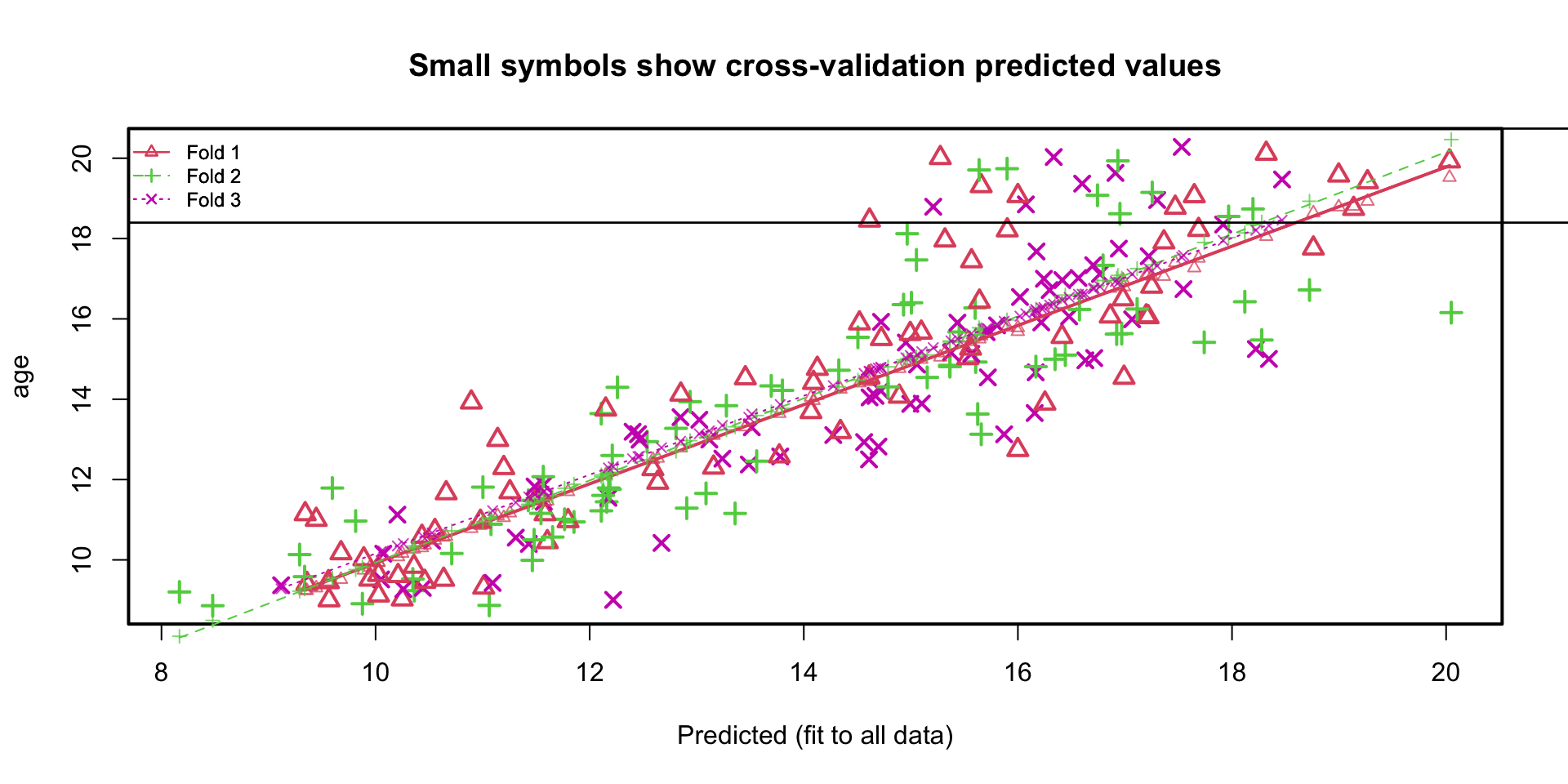
DAAG::CVlm(na.omit(boys), boys.fit5, plotit="Observed", printit=F)

Plotting the residuals

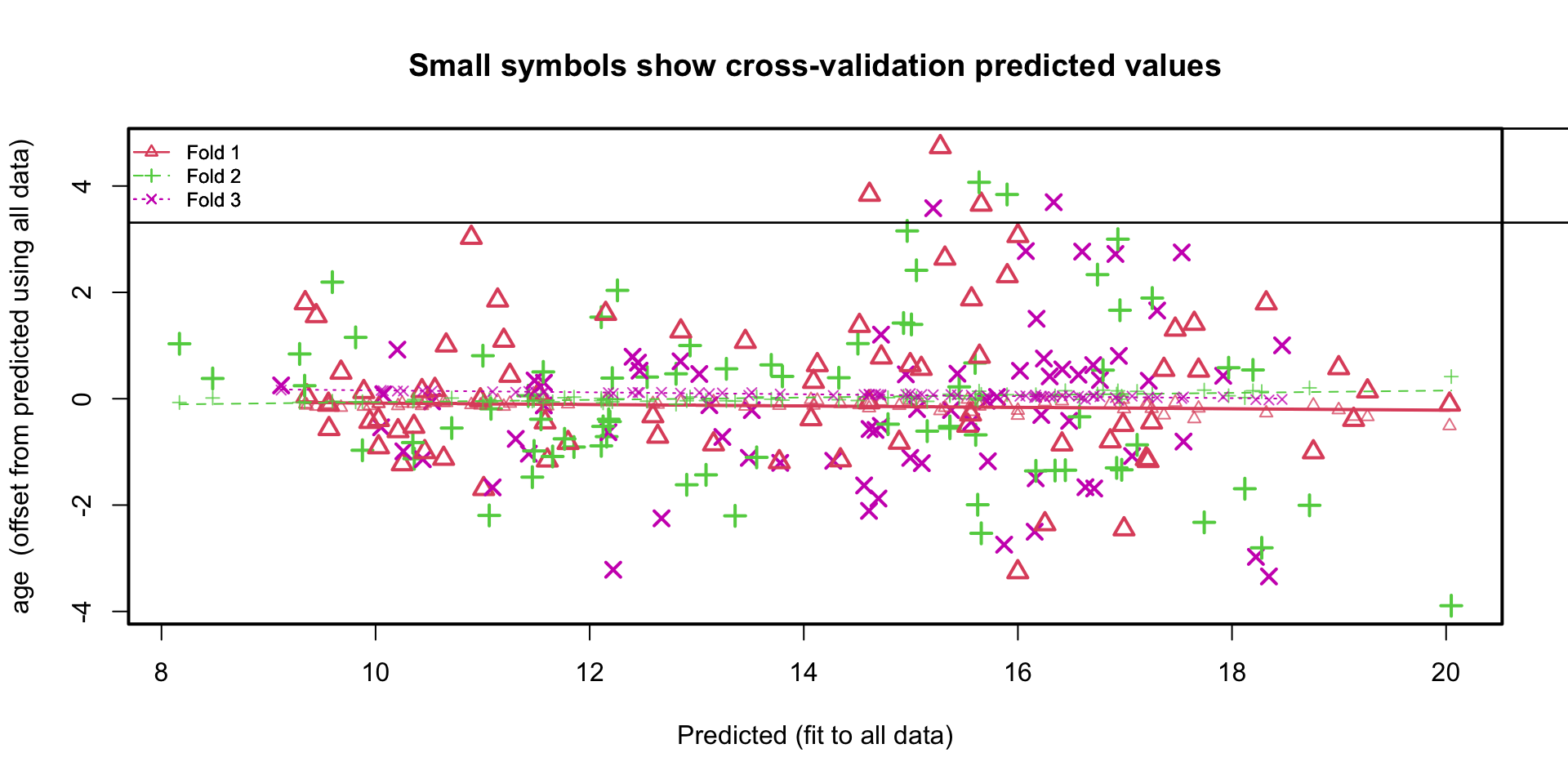
DAAG::CVlm(na.omit(boys), boys.fit5, plotit="Residual", printit=F)

How many cases are used?

na.omit(boys) %$%
  lm(age ~ reg + hgt * wgt) %>%
  nobs()

[1] 223

If we would not have used na.omit()

boys %$%
  lm(age ~ reg + hgt * wgt) %>%
  nobs()

[1] 724

Confidence intervals?

95% confidence interval

If an infinite number of samples were drawn and CI’s computed, then the true population mean \(\mu\) would be in at least 95% of these intervals

\[ 95\%~CI=\bar{x}\pm{t}_{(1-\alpha/2)}\cdot SEM \]

Example

x.bar <- 7.6 # sample mean
SEM   <- 2.1 # standard error of the mean
n     <- 11 # sample size
df    <- n-1 # degrees of freedom
alpha <- .15 # significance level
t.crit <- qt(1 - alpha / 2, df) # t(1 - alpha / 2) for df = 10
c(x.bar - t.crit * SEM, x.bar + t.crit * SEM)

[1]  4.325605 10.874395

Misconceptions

Confidence intervals are frequently misunderstood, even well-established researchers sometimes misinterpret them. .

A realised 95% CI does not mean:

that there is a 95% probability the population parameter lies within the interval
that there is a 95% probability that the interval covers the population parameter

Once an experiment is done and an interval is calculated, the interval either covers, or does not cover the parameter value. Probability is no longer involved.

The 95% probability only has to do with the estimation procedure.

A 95% confidence interval does not mean that 95% of the sample data lie within the interval.
A confidence interval is not a range of plausible values for the sample mean, though it may be understood as an estimate of plausible values for the population parameter.
A particular confidence interval of 95% calculated from an experiment does not mean that there is a 95% probability of a sample mean from a repeat of the experiment falling within this interval.

Confidence intervals

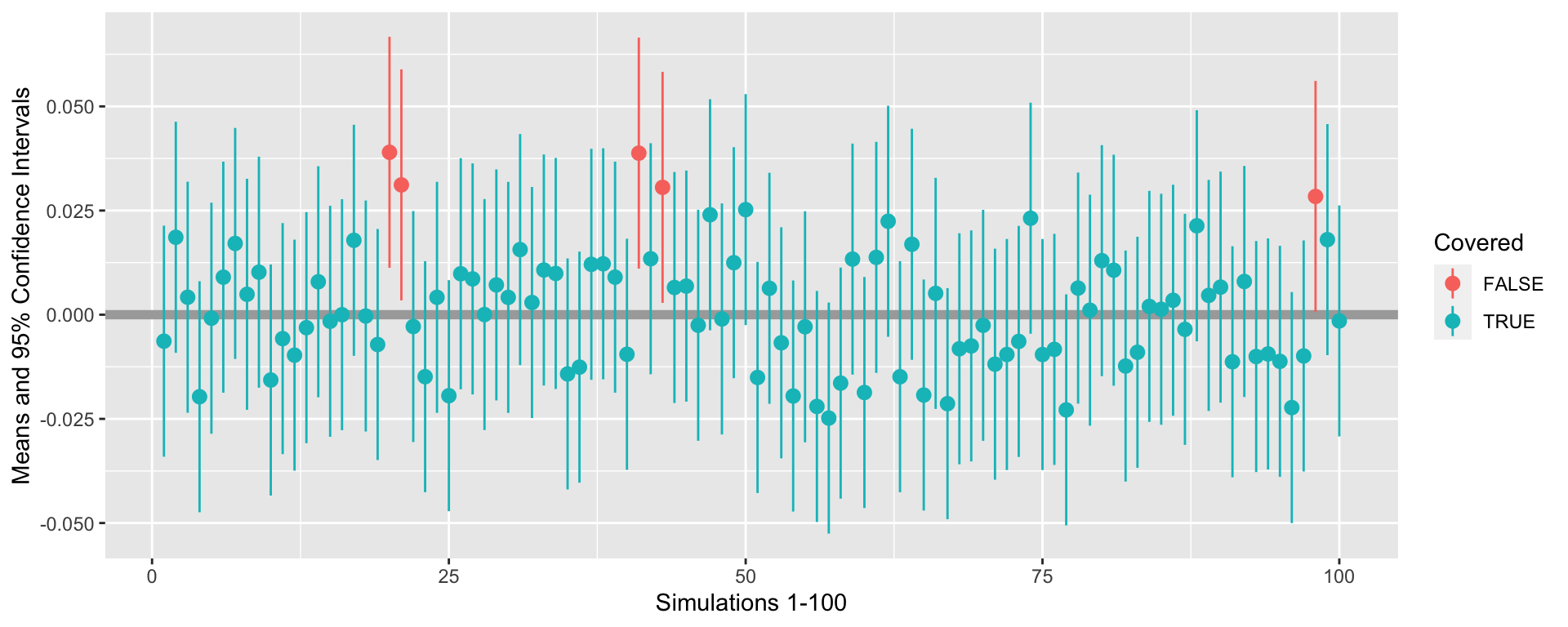
100 simulated samples from a population with \(\mu = 0\) and \(\sigma^2=1\). Out of 100 samples, only 5 samples have confidence intervals that do not cover the population mean.

For fun

source

How wrong may a useful model be?

We use the following packages

The linear model

Notation

Univariate expectation

Conditional expectation

Assumptions

The key assumptions

A simple model

Visualizing the assumptions

Visualizing the assumptions

Model fit

A simple model

Plotting the model

Model parameters

Scientific notation

Is it a good model?

AIC

What is AIC

Model comparison

A new model

Another model

And another model

Model comparison

And with anova()

Inspect boys.fit3

Inspect boys.fit4

Remove reg

Influence of cases

Prediction

Fitted values

Predict new values

Predictions are draws from the regression line

Prediction intervals

Assessing predictive accuracy

Model performance

K-fold cross-validation

The original model

K-fold cross-validation anscombe data

K-fold cross-validation anscombe data

Plotting the residuals

K-fold cross-validation boys data

K-fold cross-validation boys data

Plotting the residuals

How many cases are used?

Confidence intervals?

95% confidence interval

Misconceptions

Confidence intervals

For fun

And with `anova()`

Inspect `boys.fit3`

Inspect `boys.fit4`

Remove `reg`

K-fold cross-validation `anscombe` data

K-fold cross-validation `anscombe` data

K-fold cross-validation `boys` data

K-fold cross-validation `boys` data