library(MASS) # for the cats data library(magrittr) # pipes library(dplyr) # data manipulation library(caret) # flexible machine learning library(kernlab) # for SVM's library(e1071) # also for SVM's library(DT) # interactive tables set.seed(123) # for reproducibility
Data Science and Predictive Machine Learning
Packages used in this lecture
So far
We have learned the following techniques
- linear regression
- logistic regression
- ridge regression
- lasso regression
- the elastic net
Data
Our data has two classifications that are perfectly seperable by a hyperplane
Hyperplanes
Hyperplanes divide a \(p\)-dimensional space into two distinct parts
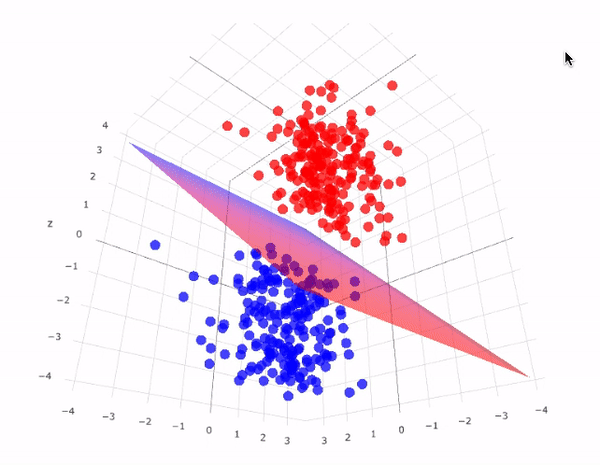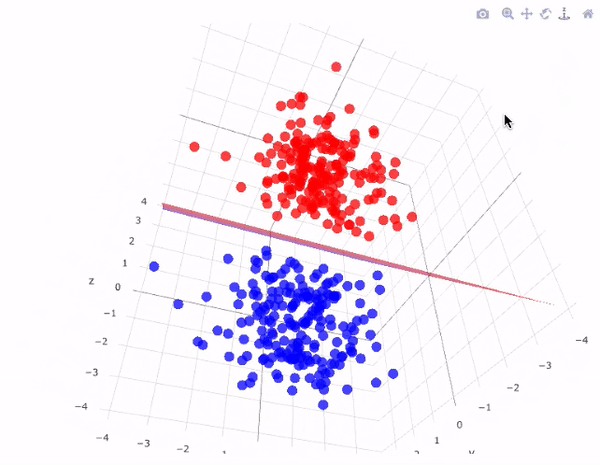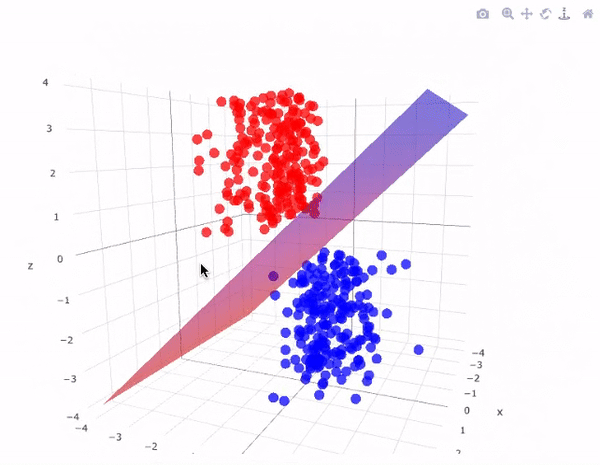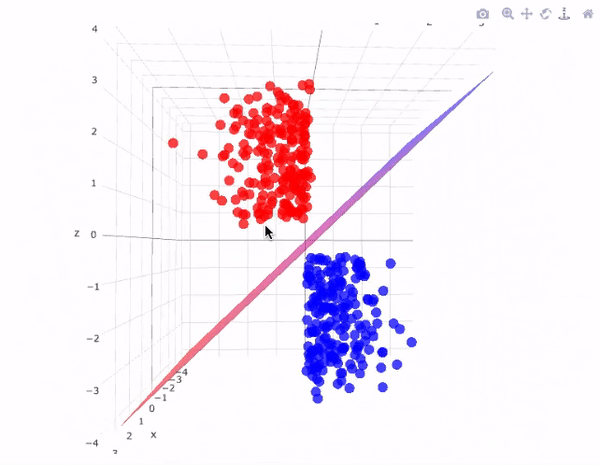
For our data
The aim for this lecture is to find the hyperplane that seperates the space into two parts.
We will explore multiple ways of doing so
But there is a problem
When data are perfectly seperable, there are infinite hyperplanes that seperate the space
Maximal Margin Classifier
The chosen hyperplane maximizes the margins (i.e. the perpendicular distance from the hyperplane)
The observations that fall on the margins are called the support vectors
Maximal Margin Classifier
The maximal margin classifier suffers from a problem: it is highly dependent on the support vectors.
Shifting, removing or adding even a single observation may lead to a dramatic change in the maximal margin hyperplane.
Inseperable classes
The maximal margin classifier is not suitable when classes are not perfectly seperable by a straight line
In that case some room for error (Cost) needs to be allowed
So far
The maximal margin classifier creates a hyperplane that maximizes the margins towards the support vectors
- It works if and only if classes are perfectly seperable
- It is highly sensitive to individual observations
- It is a so-called hard classifier
Support vector classifier
With the support vector classifier we allow for two errors: Observations may be incorrectly classified and observations may be on the wrong side of the margin.
How does it work?
Instead of minimizing the margins, we specify a total amount of error to be allowed.
To allow for individual to be on the wrong side of both the hyperplane and the margin, we define slack variables \(\varepsilon_i\).
- When \(\varepsilon_i = 0\) then the \(i\)th observation is on the correct side of the margin.
- When \(\varepsilon_i > 0\) then the \(i\)th observation is on the wrong side of the margin.
- When \(\varepsilon_i > 1\) then the \(i\)th observation is on the wrong side of the hyperplane.
You can imagine that the wider we choose the margins, the higher the sum of the \(\varepsilon_i\)’s.
To bound the sum of the \(\varepsilon_i\)’s we need a tuning parameter \(C\).
- \(C\) determines the number and severity of the violations to the margin (and to the hyperplane) that we will tolerate.
- If there is no room for violations to the margin, then it must be the case that \(\varepsilon_1 = \dots = \varepsilon_n = 0\). In that case \(C\) is large.
Choosing \(C\)
\(C\) is a tuning parameter and needs to be chosen.
- When \(C\) is small, margins will be wide. With wider margins come many support vectors and more misclassified observations.
- When \(C\) is large , margins will be narrow. With narrower margins come fewer support vectors and less misclassified values.
Just like with every technique so far it holds that lowering \(C\) may prevent overfitting. This may yield better performance on the test set.
We can again use validation techniques to find the value for \(C\) for which we minimize test error.
A good demo to play around with
Non-linear seperability
The support vector classifier is a linear classifier: It can not classify non-linearly seperable data.
So far
The maximal margin classifier creates a hyperplane that maximizes the margins towards the support vectors
- It works if and only if classes are perfectly seperable
- It is highly sensitive to individual observations
- It is a so-called hard classifier
The support vector classifier creates a hyperplane that maximizes the margins towards the support vectors
- It works if and only if classes are linearly seperable
- It is not sensitive to individual observations
- It is a so-called soft classifier
- Use \(C\) to optimize for the margins: the distance the decision boundaries have from the hyperplane.
Support vector machine
The support vector machine extends the support vectors classifier by using kernels to create non-linear decision boundaries.
Through the kernel trick it is possible to map the inputs in the original (i.e. lower dimensional space) and returns the dot product of the transformed vectors in the higher dimensional space.
It uses a kernel function. The most used are:
- linear kernel
- polynomial kernel
- radial kernel
If you want to read more about kernels, this link provides some nice easy explanation
Linear kernel
Polynomial kernel
With the polynomial kernel we need to optimize over the polynomial degree, \(C\) and the scale (variance) \(\gamma\).
Radial basis function kernel
With the radial kernel there is another optimizable parameter \(\gamma\).
Optimal \(\gamma\)
We can view \(\gamma\) as the inverse of the radius of influence of samples that are selected by the model as support vectors.
- the RBF kernel uses a Gaussian function
- low \(\gamma\) defines a Gaussian function with high variance: similarity is easier to realize between two points
- High \(\gamma\) defines a Gaussian function with low variance: similarity is harder to realize between two points - points need to have actual proximity.
Like always, \(\gamma\) can be optimized by test/train validation.
Simple example
head(cats)
## Sex Bwt Hwt ## 1 F 2.0 7.0 ## 2 F 2.0 7.4 ## 3 F 2.0 9.5 ## 4 F 2.1 7.2 ## 5 F 2.1 7.3 ## 6 F 2.1 7.6
svm.cats <- svm(Sex ~ ., data = cats, kernel = "linear", cost = 1, scale = TRUE)
Output
svm.cats
## ## Call: ## svm(formula = Sex ~ ., data = cats, kernel = "linear", cost = 1, ## scale = TRUE) ## ## ## Parameters: ## SVM-Type: C-classification ## SVM-Kernel: linear ## cost: 1 ## ## Number of Support Vectors: 78
Plot
plot(svm.cats, cats)
Plot
svm.cats <- svm(Sex ~ ., data = cats, kernel = "linear", cost = 4, scale = TRUE) plot(svm.cats, cats)
with caret and crossvalidation
train_control <- trainControl(method="repeatedcv", number=10, repeats=3)
svm.cats <- train(Sex ~.,
data = cats,
method = "svmLinear",
trControl = train_control,
preProcess = c("center","scale"))
Output from caret
svm.cats
## Support Vector Machines with Linear Kernel ## ## 144 samples ## 2 predictor ## 2 classes: 'F', 'M' ## ## Pre-processing: centered (2), scaled (2) ## Resampling: Cross-Validated (10 fold, repeated 3 times) ## Summary of sample sizes: 129, 129, 130, 130, 130, 130, ... ## Resampling results: ## ## Accuracy Kappa ## 0.7829182 0.5082337 ## ## Tuning parameter 'C' was held constant at a value of 1
Parameter \(C\) is kept constant by default.
Optimizing for \(C\)
svm.cats <- train(Sex ~.,
data = cats,
method = "svmLinear",
trControl = trainControl(method="repeatedcv", number=10, repeats=3),
preProcess = c("center","scale"),
tuneGrid = expand.grid(C = seq(0.1, 10, length = 50)))
Optimal C
plot(svm.cats)
Plot
kernlab::plot(svm.cats$finalModel)
Radial Kernel
svm.cats <- train(Sex ~.,
data = cats,
method = "svmRadial",
trControl = trainControl(method="repeatedcv", number=10, repeats=3),
preProcess = c("center","scale"),
tuneGrid = expand.grid(C = seq(0.1, 5, by = .1),
sigma = seq(0.5, 5, by = .5)))
Optimal C and \(\gamma\)
plot(svm.cats)
svm.cats$bestTune
## sigma C ## 161 0.5 1.7
Plot
kernlab::plot(svm.cats$finalModel)
Performance
pred <- predict(svm.cats) postResample(pred, cats$Sex)
## Accuracy Kappa ## 0.7986111 0.5394795
confusionMatrix(pred, cats$Sex)$table
## Reference ## Prediction F M ## F 32 14 ## M 15 83